В своей прошлой статье я рассказал о том, что не следует при размещении букмекерских ставок, полагаться только на среднюю величину, которая сильно зависит от резко отклоняющихся значений и не позволяет точно оценить разброс значения для ряда чисел.
Разброс значений можно определить разными способами, в том числе и с помощью среднеквадратического отклонения. Среднеквадратическое отклонение — это величина, которая показывает разницу между обычными значениями и средними значениями в ряде чисел. Различные исходные данные используются отдельно, либо в качестве исходных параметров для функции или распределения.
Нормальное распределение в сравнении с распределением Пуассона
Известно, что модель распределения Пуассона для прогноза количества голов забитых командой во время футбольного матча используется многими игроками. В этом распределении применяется один исходный параметр — средняя величина. Это дискретное распределение с выходными значениями в виде целых чисел.
Модель Пуассона нужно использовать скорее для непосредственной оценки шанса забыть гол, но ни как не для такого события: в период с 25-й по 30-ю минуты игры. Хотя последнее можно рассчитать с помощью расширенной модели.
Распределение Гаусса или нормальное распределение также очень часто используется при расчетах. Эта модель немного отличается от модели Пуассона. Это непрерывное распределение, которое основанное на двух параметрах: средней величине и среднеквадратическом отклонении.
Прогнозирование количества голов в рамках Premier League
Как пример давайте рассмотрим разницу голов по итогам футбольных матчей. Предположим, что для разницы голов за каждый матч действует закон нормального распределения. Разница голов — это количество голов, забитых хозяевами поля, за вычетом голов, забитых командой гостей. Ничья это нулевой показатель.
Давайте ознакомимся с результатами Premier League сезона 2013-2014 г.
- Лучшую по результативности игру на своем поле продемонстрировала команда Manchester City, обыграв Norwich с счетом 7:0
- Победа Liverpool’я с счетом 5:0, против Tottenham стала самой убедительной победой на чужом поле.
- Средняя величина голов 0.3789 (медиана и мода = 0 ).
- Величина среднеквадратического отклонения 1.9188
Исходя из этих данных можно прийти к нескольким выводам. Наиболее частым показателем при подсчете разницы голов есть ничейный результат. Достигается практически симметрическое распределение с перевесом в сторону побед на своем поле. Но эта статья посвящена в первую очередь среднеквадратическому отклонению.
Расчет среднеквадратического отклонения
Для формирования кривой нормального распределения используют два параметра: среднюю величину и среднеквадратическое отклонение. Среднеквадратическое отклонение от средней величины относится к 68% распределения, а 2 среднеквадратических отклонения к 95%.
В этом случае 68% игр завершатся с показателями от -1.5399 до 2.2977 гола. Для непрерывной кривой действуют свои ограничения: становится недопустимой разница голов с показателем -1.5399.
Для того что бы оценить победы на своем поле с помощью разницы голов, целое значение можно заменить на значение из диапазона от 0.5 до 1.5. Затем каждое значение можно сравнить с средней величиной с учетом среднеквадратических отклонений.
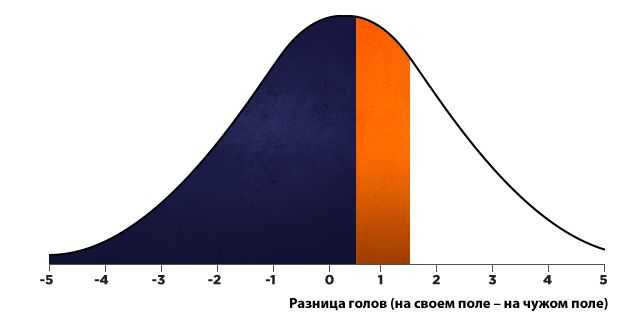
В результате у нас появляется возможность заново составить модель нормального распределения. В этом случае нам необходимо выбрать область оранжевого цвета.
Область которая выделенная синим цветом — это вероятность того, что будет забито меньше 1 гола (около 52% шанса).
Более подробный расчет не нужен, но его легко можно выполнить с помощью различных программ, например в MS Excel: =НОРМ.РАСП(0,5;0,3789;1,9188;1). Подобным образом можно рассчитать вероятность голов ниже показателя 1.5. Она находится на уровне 72.05%. Таким образом, ожидаемая разница между двумя значениями составляет 19.53%
По итогам оценки 74.22 игр из 380 завершились бы победой хозяев с разницей всего один гол. На самом деле проведены 75 игр с указанным результатом, поэтому показатель который мы получили очень близок к фактическому значению.
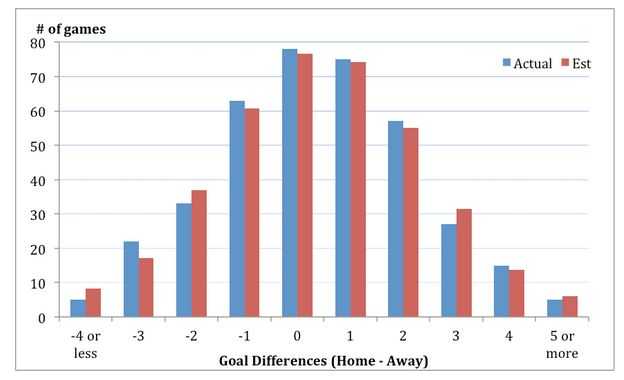
Если повторять эти действия для всех случаев с разницей голов, то можно сравнить фактическое и предположительное количество игр, которые завершились с разными показателями голов.
В таблице ниже указано минимальное расхождение — в этом случае нормальное распределение подобрано правильно. Проверку нормальности распределения можно выполнить разными способами. Описанное распределение успешно применяется для анализа статистики турника EPL 2013-2014 гг.
Допустим, распределение подходит для оценки матчей текущего сезона Premier League. Игроку, который размещает ставку с учетом разницы голов, пригодится информация о вероятности выигрыша команды хозяев поля с разницей не менее чем один гол в рамках Premier League.
По следующей форме мы можем рассчитать значение: 100% — 52.52% = 47.48%.
Это только общая оценка, которая применимая к результатам матчей Premier League в целом и не применима к достижениям отдельных команд. Игрокам следует анализировать статистику отдельных команд, а не всей лиги EPL.
Вывод
Среднеквадратическое отклонение — это не просто разброс числовых данных. Это также очень важный параметр для расчета вероятности, что крайне полезно для игроков, размещающих ставки на спортивные события. В будущих статьях рассмотрим как различное среднеквадратическое отклонение влияет на вероятность и разброс значений.